索引入门
索引入门
什么是索引
索引的出现其实就是为了提高数据查询的效率,就像书的目录一样
对于数据库的表而言,索引其实就是它的“目录”
# 常见索引模型
- 哈希KV表
- 有序数组
- 搜索树
# 哈希KV表
用一个哈希函数把 key 换算成一个确定的位置,然后把 value 放在数组的这个位置。
优点:插入速度快 缺点:查询慢,不能范围查询(就会全表扫描) 适合:NoSQL之类的等值查询
哈希碰撞时,就拉出一个链表。如图
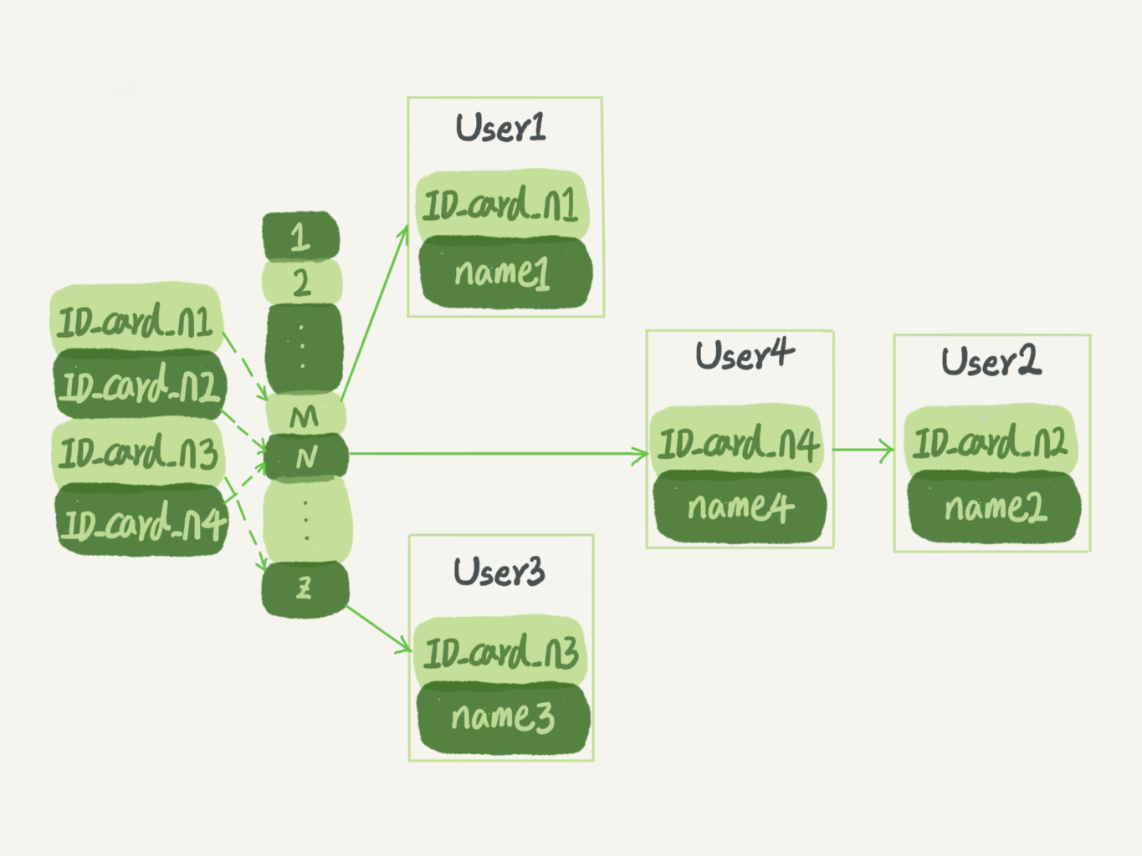
图中四个 ID_card_n 的值并不是递增的,插入方便,范围查询痛苦
# 有序数组
优点:等值查询和范围查询十分优秀 缺点:插入慢 适用:静态存储
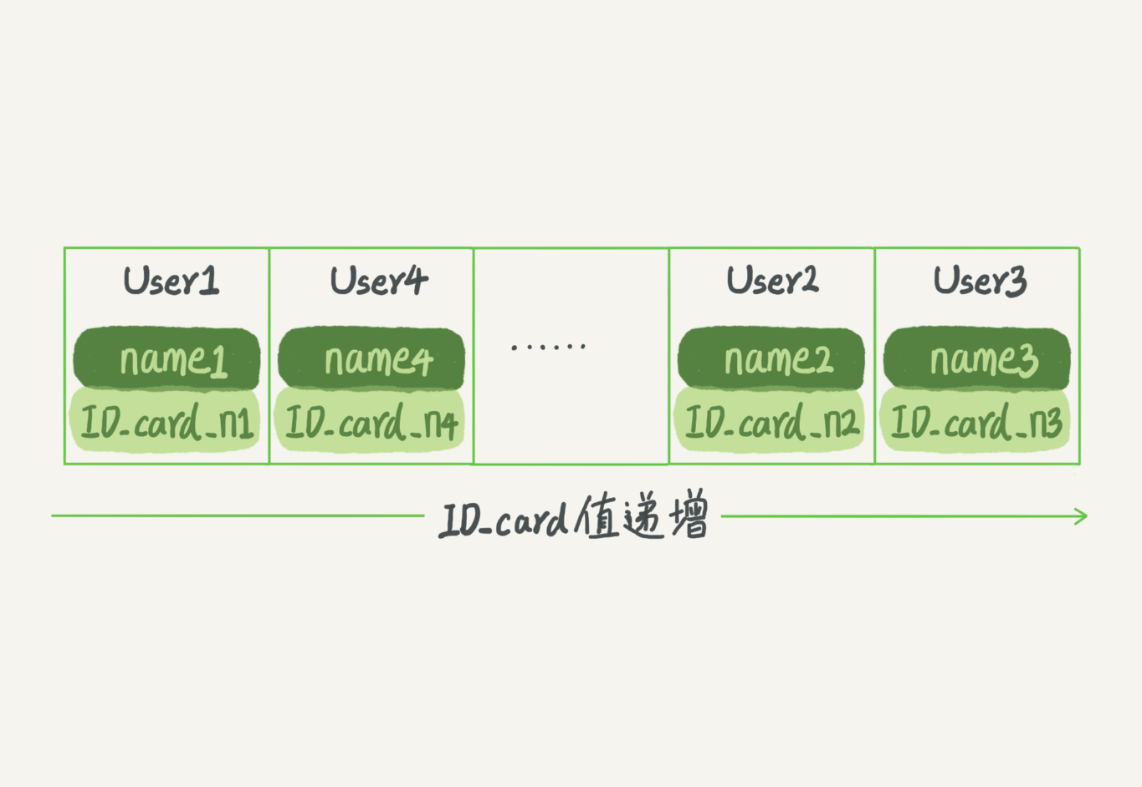
# 搜索树
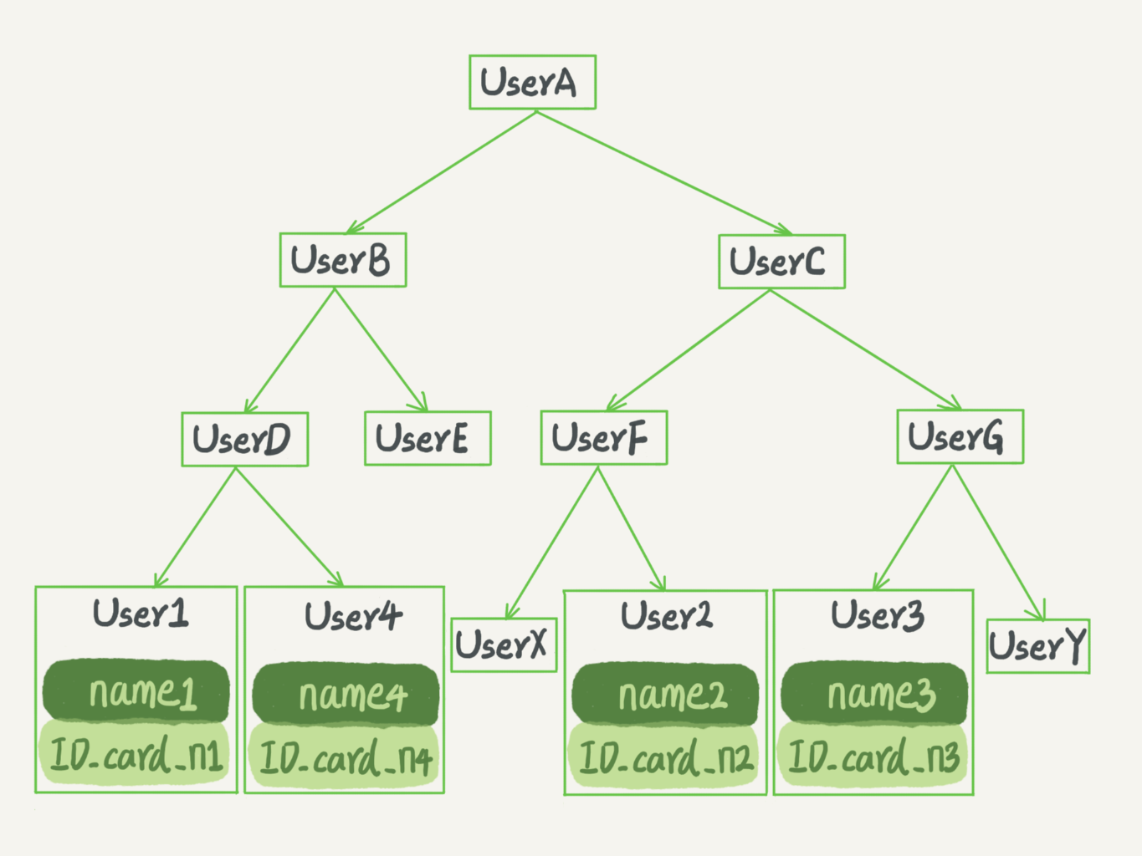
二叉搜索树的特点是:父节点左子树所有结点的值小于父节点的值,右子树所有结点的值大于父节点的值。
要查 ID_card_n2 的话,按照图中的搜索顺序就是按照 UserA -> UserC -> UserF -> User2 这个路径得到。这个时间复杂度是 O(log(N))。
为了维持 O(log(N)) 的查询复杂度,你就需要保持这棵树是平衡二叉树。为了做这个保证,更新的时间复杂度也是 O(log(N))。
# 数据库常用N叉树
二叉树搜索效率高,但是数据库中很少用,反而用多叉树
原因是,索引不止存在内存中,还要写到磁盘上。
一棵 100 万节点的平衡二叉树,树高 20。一次查询可能需要访问 20 个数据块。在机械硬盘时代,从磁盘随机读一个数据块需要 10 ms 左右的寻址时间。也就是说,对于一个 100 万行的表,如果使用二叉树来存储,单独访问一个行可能需要 20 个 10 ms 的时间,这个查询可真够慢的。
为了让一个查询尽量少地读磁盘,就必须让查询过程访问尽量少的数据块。那么,我们就不应该使用二叉树,而是要使用“N 叉”树。这里,“N 叉”树中的“N”取决于数据块的大小。
N 叉树由于在读写上的性能优点,以及适配磁盘的访问模式,已经被广泛应用在数据库引擎中了。
# InnoDB索引模型-B+树
在 InnoDB 中,表都是根据主键顺序以索引的形式存放的,这种存储方式的表称为索引组织表。
每一个索引在 InnoDB 里面对应一棵 B+ 树。
假设,我们有一个主键列为 ID 的表,表中有字段 k,并且在 k 上有索引。这个表的建表语句是:
create table T(
id int primary key,
k int not null,
name varchar(16),
index (k))engine=InnoDB;
2
3
4
5
表中 R1~R5 的 (ID,k) 值分别为 (100,1)、(200,2)、(300,3)、(500,5) 和 (600,6),两棵树的示例示意图如下。
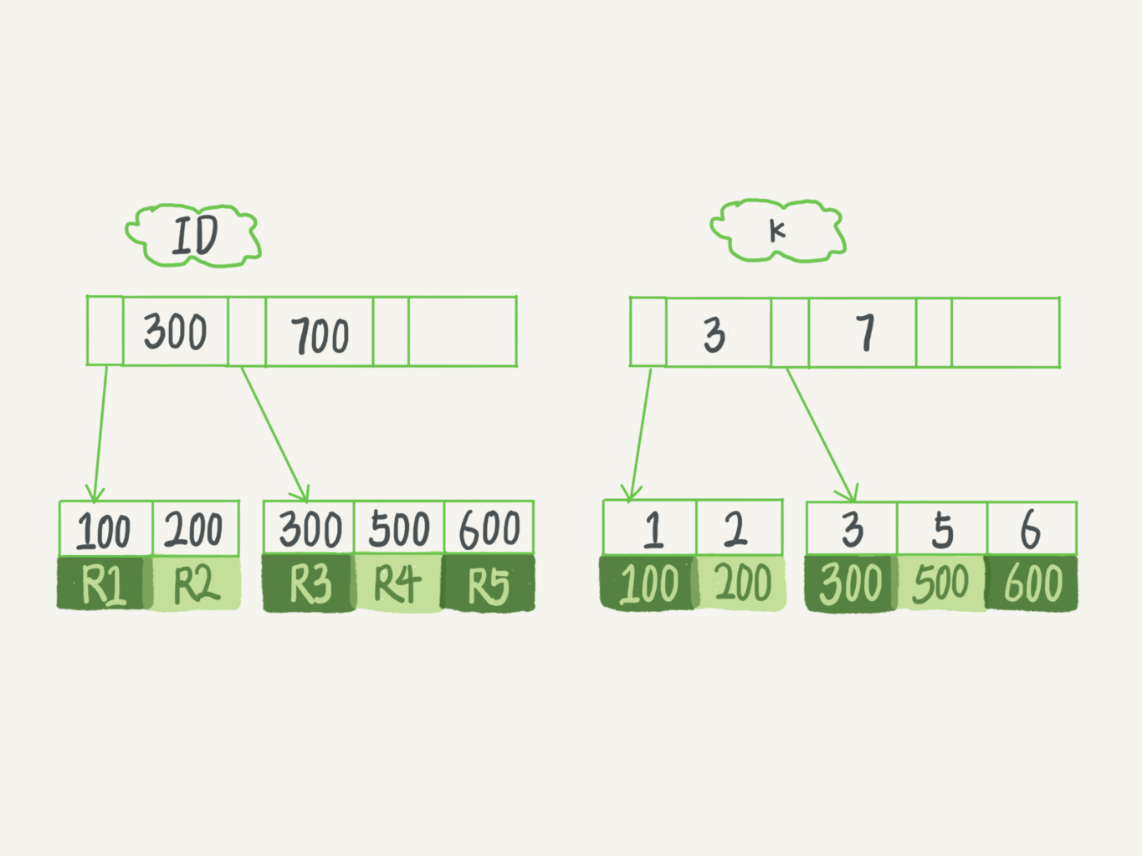 据叶子节点的内容,索引类型分为主键索引和非主键索引。
据叶子节点的内容,索引类型分为主键索引和非主键索引。
主键索引的叶子节点存的是整行数据。在 InnoDB 里,主键索引也被称为聚簇索引(clustered index)。
非主键索引的叶子节点内容是主键的值。在 InnoDB 里,非主键索引也被称为二级索引(secondary index)。
# 主键索引和普通索引区别
一个不用回表,一个要回表
如果语句是 select * from T where ID=500,即主键查询方式,则只需要搜索 ID 这棵 B+ 树;
如果语句是 select * from T where k=5,即普通索引查询方式,则需要先搜索 k 索引树,得到 ID 的值为 500,再到 ID 索引树搜索一次。这个过程称为回表
基于非主键索引的查询需要多扫描一棵索引树。因此,我们在应用中应该尽量使用主键查询。